Мы уже знаем, что такое обыкновенные дроби (см. статью здесь). А сегодня научимся сравнивать дроби с одинаковыми знаменателями.
Сравнивать обыкновенные дроби очень легко на примере предметов, ведь очевидно, что, к примеру, 1/2 часть яблока отличается от 1/4 части.

Это при условии, что предметы, разделенные на части одинаковые по размеру.
Результат сравнения обыкновенных дробей — это равны или неравны.
Если дроби не равны, обычно нужно также узнать, какая из данных дробей меньше, а какая – больше.
Когда предмет разделен на равные части, сравнение дробей (количество частей) выполняется так же, как и сравнение количества целых предметов. И сделать это очень просто.
Давайте разбираться.
1. Сравним дроби 3/5 и 2/5 . Чертим схему.

Отрезок делим на 5 одинаковых частей, потому что знаменатель — 5. И взяли 3 части, и 2 таких же части. Мы видим, что 3 части больше, чем 2 части.
Следовательно, 3/5 > 2/5 .
Сравним на другом примере:
Андрей съел 3 куска пиццы, а Света – 2 куска. Кто съел больше Андрей или Света?


Мы видим, что Андрей съел больше, значит, 3/5 > 2/5.
Что у них общего у дробей 3/5 и 2/5? Оказалось, что это дроби – с одинаковыми знаменателями.
А числители? А числители – разные: в первой дроби числитель 3, а во второй — 2. Сравним эти числа: 3 > 2 и оказалось, что дробь 3/5 больше 2/5.
2. Сравним дроби: 8/13 и 10/13.
Чертим схему:

Отрезок разделили на 13 равных частей, потому что знаменатель — 13. Одной фигурной скобкой мы объединили 8 частей, а другой фигурной скобкой объединили 10 таких же частей.
Мы видим, что 8/13 меньше 10/13.
Рассмотрим эту пару дробей: 8/13 и 10/13. Что у них общего?
Все просто – это дроби с одинаковыми знаменателями.
А числители? Числители – разные: 8 и 13.
8 меньше, чем 13. Значит, дробь 8/13 меньше дроби 10/13.
3. Сравним дроби? Какая самая большая? Какая самая маленькая?

Каждый круг разделили на 6 равных частей. В первом круге 3 части раскрасили зеленым цветом, во втором круге раскрасили 2 части, а в третьем – 4 такие части.
Наглядно видно, что в третьем круге закрашена большая часть круга, а во втором – меньшая. Значит самая большая дробь 4/6, а самая маленькая – 2/6.
Чем похожи эти три дроби? У них одинаковый знаменатель – 6, а числители разные: меньшее число – 2, значит, дробь 2/6 – самая маленькая. Большее число – 4 и дробь 4/6 – самая большая.
Чем похожи пары рассматриваемых нами дробей?
Все дроби с одинаковыми знаменателями.
Вывод:

Потренируемся:
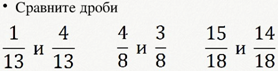
Проверка:
в первой паре дробей знаменатель одинаковый — 13, значит, сравниваем числитель: 1 меньше 4, значит, и дробь 1/13 < 4/13.
Вторая пара: знаменатель одинаковый — 8, значит, сравниваем числитель: 4 больше 3, значит, и дробь 4/8 > 3/8.
Третья пара дробей: знаменатель одинаковый — 18, значит, сравниваем числитель: 15 больше 14, значит, и дробь 15/18 > 14/18.
Знания правила сравнения дробей с одинаковым знаменателями, легко будет выполнить следующие задания:
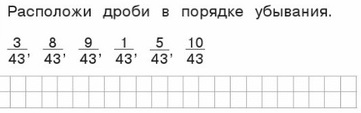
Проверка:
Это дроби с одинаковыми знаменателями, значит, сравниваем числитель: самое большое число – 10, потом – 9, 8, 5, 3, 1.
Запишем так: 10/43, 9/43, 8/43, 5/43, 3/43, 1/43.

Проверка:
это дроби с одинаковыми знаменателями, значит, сравниваем числитель: самое маленькое число – 1, потом – 4, 16, 17, 19, 20.
Запишем так: 1/24, 4/24, 16/24, 17/24, 19/24, 20/24.


